Почему у листа бумаги формата А4 такие странные размеры - 210 на 297 мм? Почему не 20 х 30 см, к примеру, что было бы куда удобнее? Листочками тогда можно было бы даже отмерять расстояния.
Для начала нужно узнать, как вообще появился лист формата А4. Это произошло путём деления листа формата А3 надвое. В свою очередь, для получения А3 нужно пополам поделить лист А2. А его, соответственно, - получили путем деления надвое листа А1. Эта площадь - половина листа формата А0.
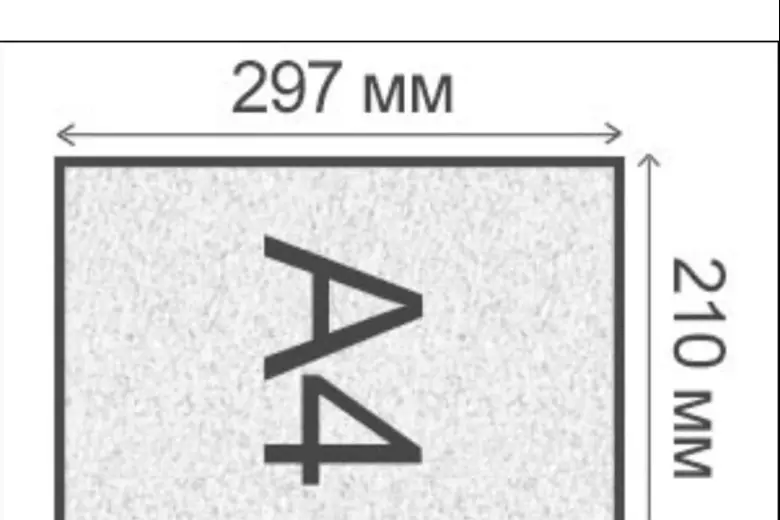
Площадь листа формата А0 составляет 1 м². Площадь А4 - в 16 раз меньше, то есть 0,0625 м². При умножении 0,21 на 0,297 получается 0,06237 - учитывая погрешность измерения линейки, это равно 0,0625. Вот и ответ на странные длины сторон листа А4.
Осталось понять: откуда берется это отношение сторон? Почему, к примеру, не 2:3? Что найти ответ, нужно рассмотреть два листа книжного формата А5. Если их положить вместе по длинной стороне, получится формат А4.
Для простоты можно обозначить стороны А5 как "х" и "y". Тогда стороны А4 будут равны "2х" и "y". Отношение данных сторон одинаково, потому можно смело записать, что х:y = y:2x. Перемножив крест на крест, получим 2х² = y², то есть y²/x² = 2,и это значит, что y : x = √2 или y = x•√2.
В самом деле, если посмотреть на соотношение 297 : 210 = 99 : 70 ≈ 1,4142, то видно, что с очень большой точностью оно равно √2.
Получается, что длинная сторона листа формата А4 относится к короткой как корень из двух к одному. И такое соотношение действует для любых форматов бумаги - А0, А1, А2, А3 и так далее.
Одинаковое соотношение всех листов бумаги стандартных форматов удобно в типографском деле.
